数値積分

💡 この記事は「コンピューターで計算する」シリーズの一部です。
1. 浮動小数点数
2. 区間演算
3. 数値積分 👈 今ここ
4. 数値微分
5. 自動微分

多くの積分は「紙とペン」で簡単に計算できるとは限りません。
実際、積分の中には

• 原始関数を初等関数で表せない

といった理由で、解析的に解くことが難しいものが多数存在します。

そのため、コンピューターを用いて積分を数値的に近似して求める手法(数値積分) が重要になります。
数値積分では、関数の値を離散的に評価し、それらを小さな面積の総和として積み上げることで積分を近似します。

数値積分(Numerical Integration)

与えられた関数の定積分の値を、解析的(紙とペンを使って式変形などを行う厳密な計算) ではなく、コンピューターを使って数値的に近似値を求める方法を数値積分(Numerical Integration) と呼びます。

特に次のような場合に有効です

• 解析的に積分できない関数を扱いたいとき
• 関数が複雑で厳密な解を求めるのが困難なとき
• 関数の式がなく、離散的なデータ点しか存在しないとき

コンピューターは繰り返しの計算を高速かつ正確に行うことが得意です。
積分区間を細かい区間に分割し、それぞれの部分の面積を求めて足し合わせる処理も素早く行うことができます。

解析的に積分が出来ない例

解析的に積分することが困難な例として、次のような積分があります。

$$\begin{aligned} \int^{\frac{\pi}{2}}_{0} \frac{d \theta}{\sqrt{1 - 0.5 \sin^{2} \theta }} \end{aligned}$$

この積分の被積分関数は、初等関数で表現できる原始関数を持ちません。
このタイプの積分は数学的に特別な形をしており、実は楕円積分(Elliptic Integral) と呼ばれる「特殊関数」に分類されるものです。

つまり、普通の関数(多項式・指数関数・三角関数など)をどれだけ組み合わせても、原始関数を表現することはできないため、解析的に解くことができません。

そのため、値を求める方法の一つとして

• 数値積分を用いて近似値を求める

が用いられることがあります。

解析的に積分できる関数は意外と限られており、現代では数値積分が極めて重要な役割を果たしています。

数値積分法

この記事では次の数値積分法を紹介します。

• 台形公式(Trapezoidal Rule)
• 二重指数関数型積分公式(DoubleExponentialFormula)

台形公式は最も基本的で理解しやすい数値積分法であり、多くの手法の基礎となります。
一方、DE法(二重指数関数型積分公式)は、積分区間の端点に特異点(関数値が無限大に発散する点) を持つ関数に対しても高精度な結果を得られる強力な手法です。

それぞれの手法の特徴・利点について、わかりやすく解説していきます。

台形公式(Trapezoidal Rule)

台形公式は、台形の面積を求める公式

$$\begin{aligned} \frac{(\text{上底} + \text{下底}) \times \text{高さ}}{2} \end{aligned}$$

に基づいて、定積分の値を台形の面積の和として近似する手法です。

積分区間をいくつかの小さな区間に分割し、各区間で関数の値を「上底」と「下底」 、小区間の区間幅を「高さ」 とみなすことで、曲線のある面積を台形の集まりとして近似します。

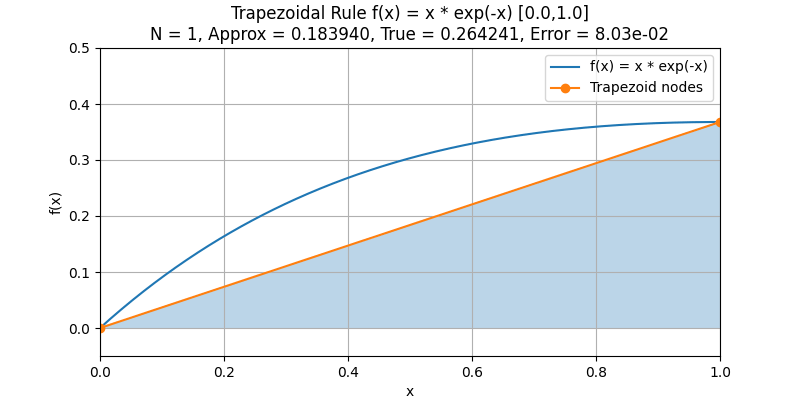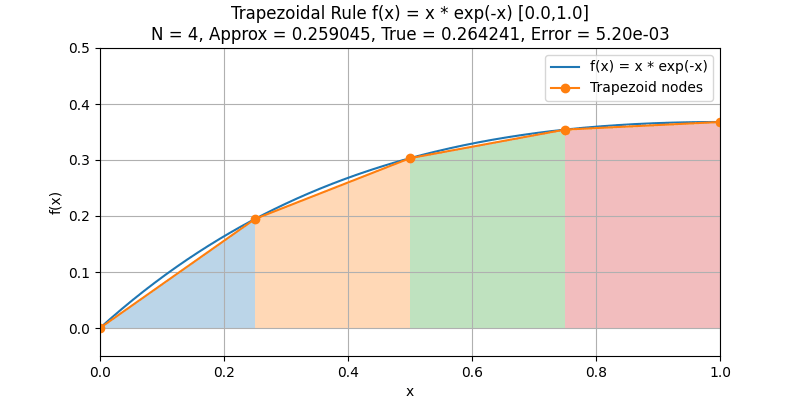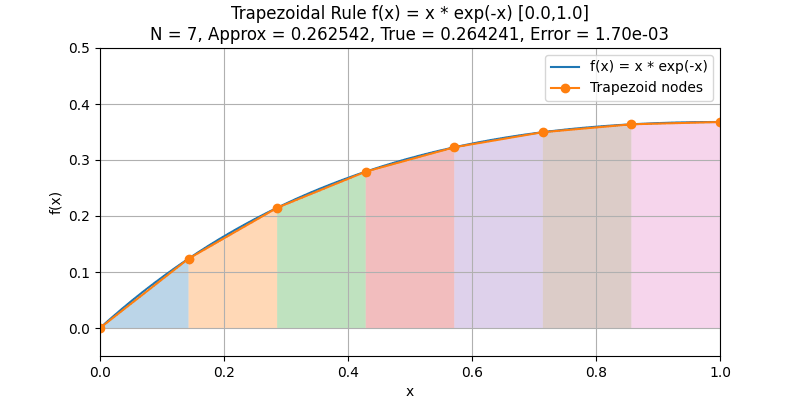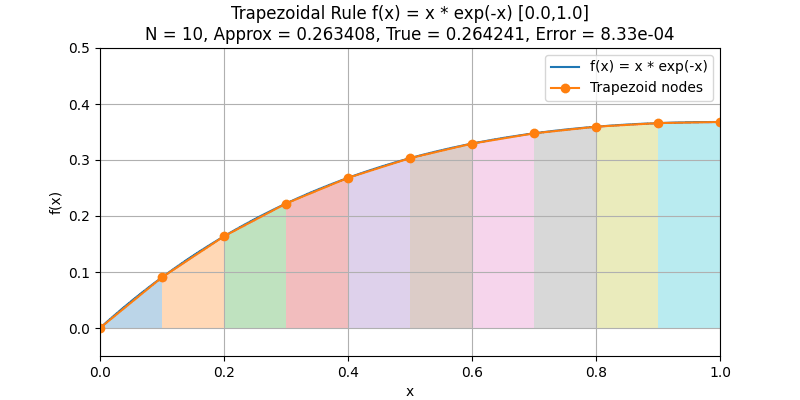
複合台形公式(Composite Trapezoidal Rule)

積分区間$[a,b]$を等間隔の小区間に分割し、その各区間に積分則を適用する方法を複合則と呼びます。
特に、各小区間に台形公式を適用し、それらを足し合わせたものを複合台形公式(Composite Trapezoidal Rule) といいます。

積分区間を$n$個の等間隔の小区間に分割し、各区間に台形公式を適用して得られる近似値を$T_{n}$とすると

$$\begin{aligned} \int_{a}^{b} f(x)dx \approx T_{n} \end{aligned}$$

となります。

$T_{n}$の具体的な式

小区間(刻み幅)を

$$\begin{aligned} h = \frac{b - a}{ n } \end{aligned}$$

とすると、複合台形公式は次のように表されます。

$$\begin{aligned} T_{n} \approx h \times \left( \frac{f(a)}{2} + \sum_{i=1}^{n-1}f( a + hi ) + \frac{f(b)}{2} \right) \end{aligned}$$

ここで

$$\begin{aligned} \frac{f(a)}{2} + \sum_{i=1}^{n-1}f( a + hi ) + \frac{f(b)}{2} \end{aligned}$$

は全ての台形の上底と下底の総和に対応し

$$\begin{aligned} h \end{aligned}$$

は台形の高さに対応します。

離散化(Discretization)

このように、元々連続的な値で定義されている関数$f(x)$を

$$\begin{aligned} f(a) \quad,\quad f(a + h) \quad,\quad f(a + 2h) \quad,\quad \dots \quad,\quad f(b) \end{aligned}$$

という離散的な点によって近似的に扱うことを離散化(Discretization) と呼びます。

台形公式の実装

次のPythonの例は、複合台形公式を用いて

$$\begin{aligned} \int_{0}^{1} x\exp(x)dx = 1 \end{aligned}$$

の定積分を近似する方法を示したものです。

import numpy as np

# 被積分関数 f(x) = x * exp(x)
def f(x):
    return x * np.exp(x)

# 複合台形公式
def trapezoidal_rule(f, a, b, n):
    h = (b - a) / n
    # aからbまでn+1個の等間隔の点を生成
    x = np.linspace(a, b, n + 1)
    y = f(x)
    # y[0]とy[-1]は端点の関数値、f(a)とf(b)
    # [1:-1](a<b)の範囲の点での関数値の和を計算
    approx = h * (0.5 * y[0] + y[1:-1].sum() + 0.5 * y[-1])
    return approx

def main():
    a, b = 0.0, 1.0  # 積分区間
    # 真値 (解析的に求めたときの値)
    true_value = 1.0

    # 分割数nのリスト
    n_values = [2, 4, 8, 16, 32, 64, 128]

    print("f(x) = x * exp(x) on [0, 1]")
    print("n\t approx\t\t error")
    print("-" * 35)

    for n in n_values:
        approx = trapezoidal_rule(f, a, b, n)
        error = abs(true_value - approx)
        print(f"{n}\t {approx:.10f}\t {error:.2e}")

if __name__ == "__main__":
    main()

実行結果

f(x) = x * exp(x) on [0, 1]
n        approx          error
-----------------------------------
2        1.0917507748    9.18e-02
4        1.0230644791    2.31e-02
8        1.0057741074    5.77e-03
16       1.0014440271    1.44e-03
32       1.0003610380    3.61e-04
64       1.0000902615    9.03e-05
128      1.0000225655    2.26e-05

分点数$n$を増やし刻み幅$h$を細かくするにつれて、台形公式の近似値が真値1に収束していく様子がよくわかります。

数値積分では、一般に分点数を増やすことで精度を上げるというアプローチをとります。しかし、分割数を増やせばその分だけ計算回数も増加し、コンピューター上では丸め誤差が蓄積してしまいます。

したがって、単純に分割数を増やすだけでは限界があり、分点数を増やした時に高速に収束する高精度な積分法が求められます。

その代表的な手法がDE公式(Double Exponential Formula, 二重指数関数型積分公式) です。

二重指数関数型積分公式(Double Exponential Formula)

二重指数関数型積分公式(DE公式)は、台形公式をベースとしながらも、特別な変数変換を行うことで非常に高速な収束 を実現する積分法です。
従来の数値積分法と比べ、次のような大きなメリットがあります。

• 分点数を増やした際の収束が非常に速く、高精度な結果が得られる
• 被積分関数が積分区間の端点(無限に発散する点)を持っていても適用できる
• 無限区間や半無限区間の積分にも自然に拡張できる

これらの特性により、DE公式は現代の数値積分手法の中でも特に強力で、科学技術計算や統計、計算物理など幅広い分野で用いられています。

DE公式(Double Exponential Formula)の計算手順

DE公式は、積分区間の端点に特異性を持つ関数や、無限区間の積分を高精度で計算するための強力な手法です。
その計算は次の2段階で行われます。

1. 元の積分に対して変数変換（DE変換）を行う

   • 変数変換 $x = \phi(t)$ により、積分区間を $(-\infty, \infty)$ に写す。
   • もとの積分区間の端点にある特異性は、変数変換後には「無限遠点（非常に遠い位置）」へ押し出される。

2. 変数変換後の積分に台形則を適用する

   • 変換後の被積分関数は、$|t|$ が大きくなるにつれて 二重指数的に減衰（急激に 0 に近づく） 。
   • このため、台形則による数値積分の収束が非常に速くなる。

変数変換によって積分は次の形になる

$$\begin{aligned} \int_{a}^{b} f(x)dx = \int_{-\infty}^{\infty} f(\phi(t))\phi^{\prime}(t) dt \end{aligned}$$

この積分に台形則を適用すると

$$\begin{aligned} \int_{a}^{b} f(x)dx &\approx h \sum_{i=-n}^{n} f(\phi(ih))\phi^{\prime}(ih)\\ h &= \frac{\log(3n)}{n} \end{aligned}$$

変換後の変数の高速な減衰によって極めて精度の高い数値積分 が得られます。

DE変換

有限区間$[a,b]$

積分区間が有限な区間$[a,b]$である場合は次のように変換します。

$$\begin{aligned} \int_{a}^{b} f(x)dx &= \int_{-\infty}^{\infty} f(\phi(t))\phi^{\prime}(t) dt\\ \phi(t) &= \frac{b - a}{2} \tanh \left( \frac{\pi}{2}\sinh(t) \right) + \frac{a + b}{2}\\ \phi^{\prime}(t) &= \frac{b - a}{4} \frac{\pi \cosh(t)}{\cosh^{2} \left( \frac{\pi}{2}\sinh(t) \right)} \end{aligned}$$

$\phi(t)$ は

$$\begin{aligned} \phi(t) \to a\qquad &,\qquad(t \to -\infty)\\ \phi(t) \to b\qquad &,\qquad(t \to \infty) \end{aligned}$$

のように、$t \to -\infty$ で $a$、$t \to +\infty$ で $b$ に近づきます。

また、被積分関数の積分区間の端点にある特異点を「無限遠へ押し出す」本当の理由は $\phi^{\prime}(t)$ にあります。
$\phi^{\prime}(t)$ は $|t| \to \infty$ で二重指数的(かなり急激) に $0$ に減衰します。

そのため、元々は積分区間の端点 $(a, b)$ に存在していた特異性は、変換後の積分では「無限遠に押し出され、積分にほとんど寄与しない」という扱いやすい形へ変換されます。

桁落ちで結果がNaNになることがある

この式は$t \to -\infty$で二重指数的(かなり急激)に $-1$へ近づいて、$t \to \infty$で二重指数的(かなり急激)に $1$へ近づいていきます。

$$\begin{aligned} \tanh \left(\frac{\pi}{2}\sinh(t) \right) \end{aligned}$$

そのため

$$\begin{aligned} \tanh(u) &- 1\\ \tanh(u) &+ 1 \end{aligned}$$

のような式が 浮動小数点の桁落ち を引き起こすことがあります。
台形測のループの中でループの端点付近で桁落ちが発生したことで、結果がNaNになることもあります。

桁落ちが発生した場合の対処法として、$\tanh \left(\frac{\pi}{2}\sinh(t) \right)-1$または $\tanh \left(\frac{\pi}{2}\sinh(t) \right)+1$ のような形にならないように、式変形を行うことで対処することができます。

また、ここで使用されている特殊関数$\sinh(x)$、$\cosh(x)$、$\tanh(x)$は双曲線関数(hyperbolic function) とよばれ、それぞれ次のように定義されています。

$$\begin{aligned} \sinh(x) &= \frac{\exp(x) - \exp(-x)}{2}\\ \cosh(x) &= \frac{\exp(x) + \exp(-x)}{2}\\ \tanh(x) &= \frac{\sinh(x)}{\cosh(x)} = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)} \end{aligned}$$

半無限区間$[a,\infty)$

積分区間が半無限区間$[a,\infty)$である場合は次のように変換します。

$$\begin{aligned} \int_{a}^{\infty} f(x)dx &= \int_{-\infty}^{\infty} f(\phi(t))\phi^{\prime}(t) dt\\ \phi(t) &= a + \exp \left(\frac{\pi}{2}\sinh(t) \right)\\ \phi^{\prime}(t) &= \frac{\pi}{2}\cosh(t)\exp \left(\frac{\pi}{2}\sinh(t) \right) \end{aligned}$$

$\phi(t)$ は

$$\begin{aligned} \phi(t) \to a\qquad &,\qquad(t \to -\infty)\\ \phi(t) \to \infty\qquad &,\qquad(t \to \infty) \end{aligned}$$

のように、$t \to -\infty$ で $a$、$t \to +\infty$ で $\infty$ に近づきます。

積分区間が$(\infty,b]$の場合

$$\begin{aligned} \int_{a}^{b} f(x)dx = -\int_{b}^{a} f(x) dx \end{aligned}$$

を使います。つまり

$$\begin{aligned} \int_{-\infty}^{b} f(x)dx = -\int_{b}^{\infty} f(x) dx \end{aligned}$$

として公式を適用して計算を行います。

変数変換前の被積分関数が指数的減衰を持つ場合

変数変換前の積分が既に指数的減衰特徴を持つ場合は次のように変換します。

$$\begin{aligned} \phi(t) = \exp(t - \exp( -t)) \end{aligned}$$

積分区間が$(-\infty, \infty)$の場合

積分区間が半無限区間$(-\infty,\infty)$である場合は次のように変換します。

$$\begin{aligned} \int_{-\infty}^{\infty} f(x)dx &= \int_{-\infty}^{\infty} f(\phi(t))\phi^{\prime}(t) dt\\ \phi(t) &= \sinh \left(\frac{\pi}{2}\sinh(t) \right)\\ \phi^{\prime}(t) &= \frac{\pi}{2}\cosh(t)\cosh \left(\frac{\pi}{2}\sinh(t) \right) \end{aligned}$$

$\phi(t)$ は

$$\begin{aligned} \phi(t) \to \infty\qquad &,\qquad(t \to -\infty)\\ \phi(t) \to \infty\qquad &,\qquad(t \to \infty) \end{aligned}$$

のように、$t \to -\infty$ で $-\infty$、$t \to +\infty$ で $\infty$ に二重指数的に近づきます。

DE公式の具体例

次の積分

$$\begin{aligned} \int_{0}^{1} \frac{dx}{\sqrt{x}} = 2 \end{aligned}$$

にDE公式を適用します。
この積分の真値は$2$であり、被積分関数$\frac{1}{\sqrt{x}}$は積分区間の端点$x=0$で特異性を持ちます。

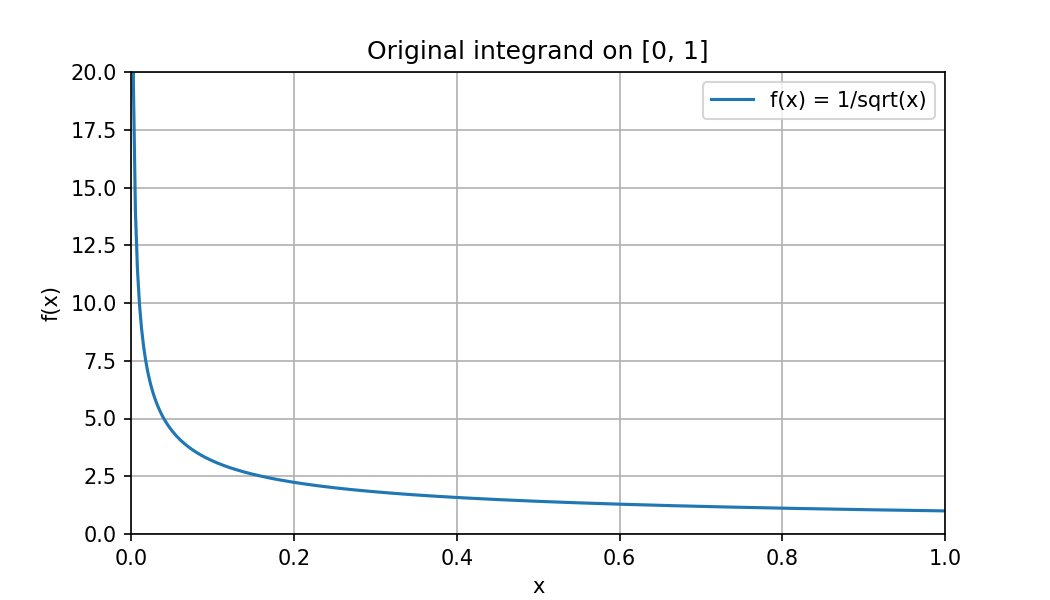
この画像のように、$x$が$0$に近づくにつれて$f(x)$が発散していることがわかります。
台形公式では、$x$が$0$に近づくにつれて$f(x)$が$\infty$に発散することで、扱える範囲の値を超えてしまい、このような積分をうまく計算することができません。

この積分

$$\begin{aligned} \int_{0}^{1} f(x)dx \end{aligned}$$

$$\begin{aligned} f(x) = \frac{1}{\sqrt{x}} \end{aligned}$$

にDE変換を適用することで

$$\begin{aligned} \int_{-\infty}^{\infty} &g(t) dt\\ g(t) &= \frac{\phi^{\prime}(t)}{\sqrt{\phi(t)}}\\ \phi(t) &= \frac{1}{2} \left(\tanh \left(\frac{\pi}{2}\sinh(t) \right) + 1\right)\\ \phi^{\prime}(t) &= \frac{\pi \cosh(t)}{4 \cosh^{2} \left(\frac{\pi}{2}\sinh(t) \right)} \end{aligned}$$

のような積分に変換されます。
DE変換後のこの被積分関数をグラフにすると

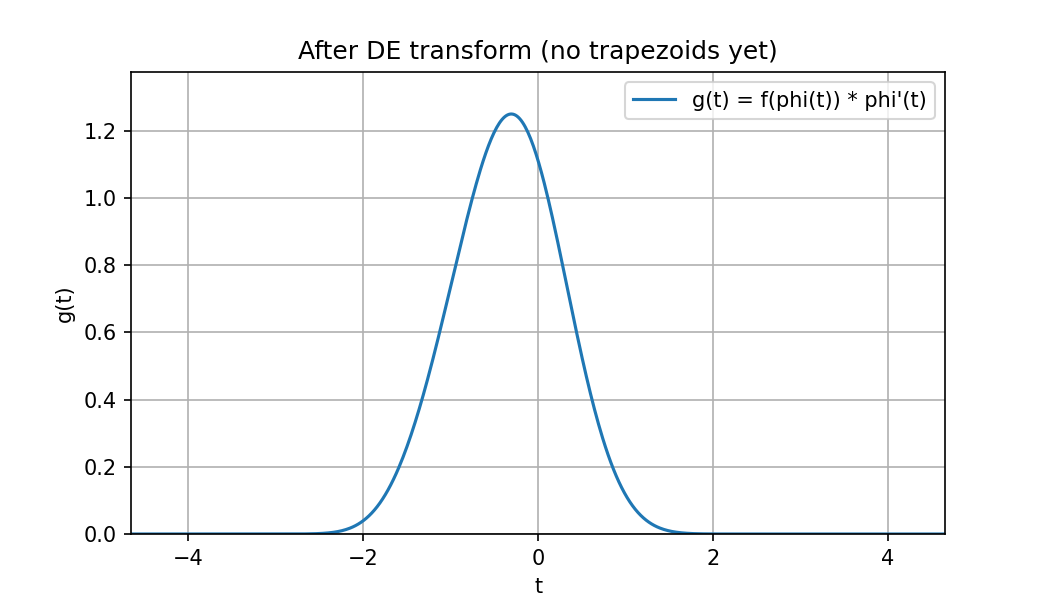
のように$|t| \to \infty$ で急激に0に近づく(二重指数的に減衰) していることがわかります。

これに、台形則を次のように適用します。

$$\begin{aligned} h\sum_{i=-n}^{n} g(ih) \end{aligned}$$

$$\begin{aligned} g(ih) = \frac{\pi \cosh(ih)}{4 \cosh^{2}\left(\frac{\pi}{2}\sinh(ih)\right)\sqrt{\frac{1}{2} \left(\tanh \left(\frac{\pi}{2}\sinh(ih) \right) + 1\right)}} \end{aligned}$$

$$\begin{aligned} h &= \frac{\log(3n)}{n} \end{aligned}$$

このようにDE変換をした後に、台形則を適用して、分点数$n$を大きくしながら計算を行う様子をグラフにすると、次のようになります。

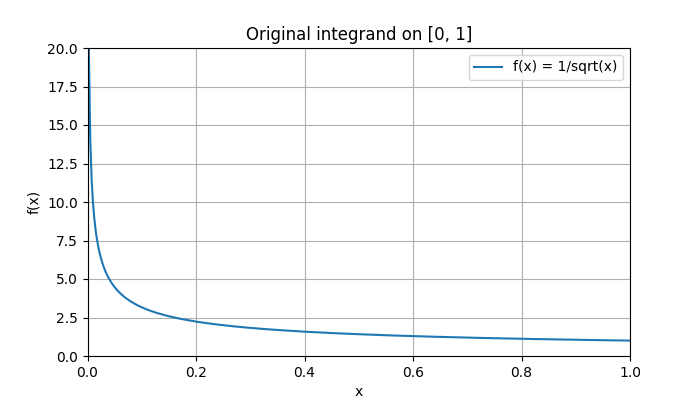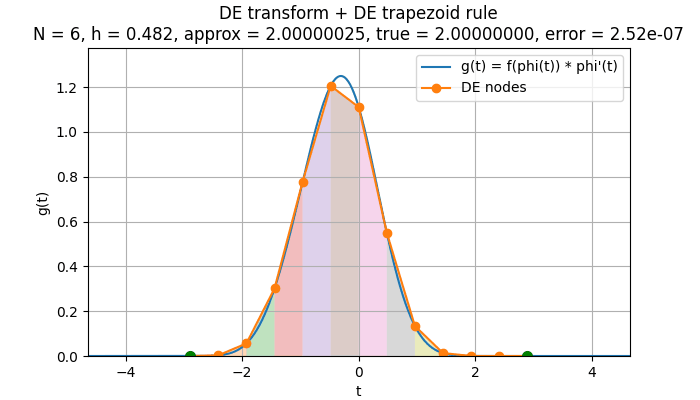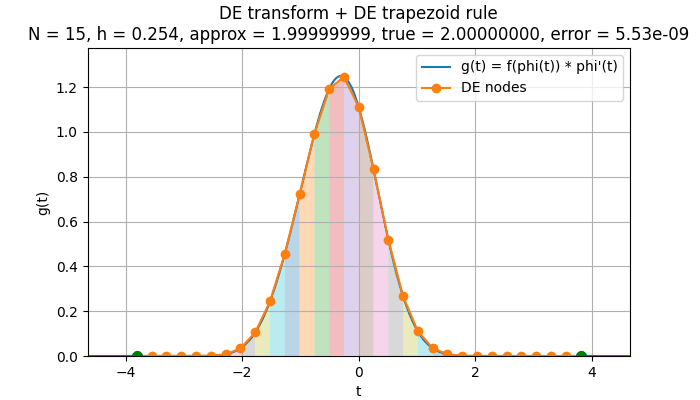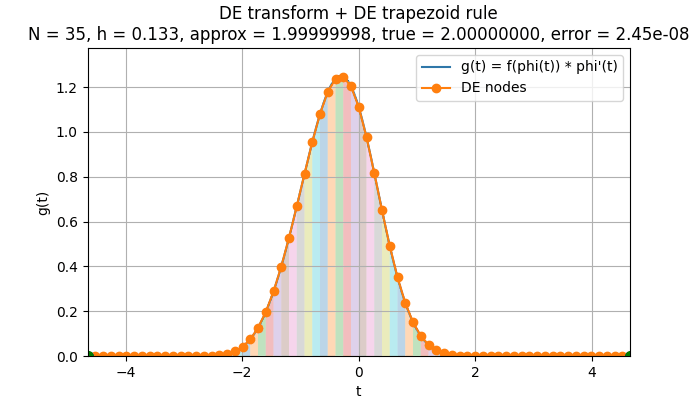
上のアニメーションからわかるように、DE変換後に適用する台形則は、通常の台形則とまったく同じ動作をしているわけではありません。

分点数 $n$ を増やすとき、台形則の分割が細かくなるだけでなく、数値積分を行う区間そのものが徐々に広がっています 。

これは、DE変換によって積分が

$$\begin{aligned} \int_{-\infty}^{\infty} g(t),dt \end{aligned}$$

という無限区間の積分に変換されているためで、実際の数値計算では

$$\begin{aligned} t \in [-nh,\ nh] \end{aligned}$$

の有限区間を切り出して台形則を適用しています。

分点数$n$が増えるとともにこの区間が外側へ広がるため、DE公式の収束には「刻み幅が小さくなる効果」(離散化誤差の減少)と「無限区間をより広く含める効果」(切り捨て誤差の減少)の両方が寄与しています。

DE公式では、分点数$n$を増やすと 「刻み幅が小さくなる（離散化誤差が減る）」 と 「積分区間が広がる（切り捨て誤差が減る）」 の2つの効果が同時に進みます。

この2つの誤差は、DE変換後の被積分関数$g(t)$の二重指数的な減衰 によって、 常に同じくらいの大きさ に保たれるよう設計されています。

その結果、誤差全体が $\exp(-cn)$のように指数的に減衰し、通常の台形公式と比べて圧倒的に速い収束 が得られます。

DE公式の実装例

次の積分をDE(Double Exponential)公式で計算します。

$$\begin{aligned} \int_{0}^{1} \frac{dx}{\sqrt{x}} = 2 \end{aligned}$$

この積分の被積分関数

$$\begin{aligned} f(x) = \frac{1}{\sqrt{x}} \end{aligned}$$

は、区間の端点$x=0$に特異性を持つため、通常の台形公式では正しく扱うことができません。

DE公式では

1. 変数変換$x = \phi(t)$により、端点の特異性を無限遠にとばす
2. 二重指数的に減衰する関数に変換された後で台形測を適用

という流れで効率的に数値積分を行います。

桁落ちを避けるための式変形

DE変換を適用してそのまま計算をすると

• $\tanh(…) - 1$のような危険な差による桁落ち
• 部分的に巨大な値が発生することでオーバーフロー

などの原因によって、結果がNaNやInfになってしまうことがあります。
今回の実装例はその典型例です。

そこで、正負で場合分けしたロジスティック関数

$$\begin{aligned} \sigma(x) = \frac{1}{1+e^{-x}} \end{aligned}$$

を用いて安全に計算しています。

pythonで実装すると次のようになります。

import numpy as np

# ---- 被積分関数 f(x) = 1/sqrt(x) ----


def f(x):
    return 1.0 / np.sqrt(x)


# ---- ロジスティック関数（符号で安定化） ----
def logistic(z):
    # σ(z) = 1 / (1 + exp(-z)) を桁落ち・オーバーフローしないように計算
    out = np.empty_like(z)
    pos = z >= 0
    neg = ~pos

    # z >= 0 のとき: exp(-z) は 0～1 に収まるので安全
    out[pos] = 1.0 / (1.0 + np.exp(-z[pos]))
    # z < 0 のとき: exp(z) は 0～1 に収まるので安全
    ez = np.exp(z[neg])
    out[neg] = ez / (1.0 + ez)
    return out


# ---- DE変換 φ(t) と φ'(t)（両方とも安定版） ----
def phi_and_phi_prime(t):
    # u = (π/2) sinh(t)
    u = (np.pi / 2.0) * np.sinh(t)
    z = 2.0 * u  # = π sinh(t)

    s = logistic(z)         # s = σ(z) = φ(t)
    phi = s                 # φ(t) 自体が σ(z)

    # φ'(t) = π cosh(t) * s * (1 - s)
    dphi = np.pi * np.cosh(t) * s * (1.0 - s)
    return phi, dphi


# ---- DE公式で積分を計算 ----
def de_integrate(n):
    # 刻み幅 h = log(3n) / n
    h = np.log(3.0 * n) / n
    total = 0.0

    for k in range(-n, n + 1):
        t = k * h
        x, dphi = phi_and_phi_prime(t)
        total += f(x) * dphi

    return h * total


def main():
    true_value = 2.0
    n_values = [4, 8, 16, 32, 64, 128]

    print("DE integration of ∫0^1 dx/√x (with underflow/cancellation-safe transform)")
    print(" n       approx            error")
    print("-------------------------------------------")

    for n in n_values:
        approx = de_integrate(n)
        error = abs(approx - true_value)
        print(f"{n:3d}   {approx: .12f}   {error:.3e}")


if __name__ == "__main__":
    main()

実行結果

 n       approx            error
-------------------------------------------
  4    2.000012041343   1.204e-05
  8    2.000000004154   4.154e-09
 16    2.000000000000   2.220e-15
 32    2.000000000000   4.441e-16
 64    2.000000000000   4.441e-16
128    2.000000000000   1.554e-15

台形公式とDE公式の特徴の比較

台形公式とDE公式の特徴を比較すると次のようになります。

台形公式とDE公式の誤差の減衰を比較

次の定積分を、台形公式とDE公式で計算して誤差の減衰を比較します。

$$\begin{aligned} \int_{0}^{1} e^{x} dx = e - 1 \end{aligned}$$

Trapezoidal rule(台形公式)とDE rule(二重指数関数型積分公式)の誤差の減衰を対数グラフで比較しています。

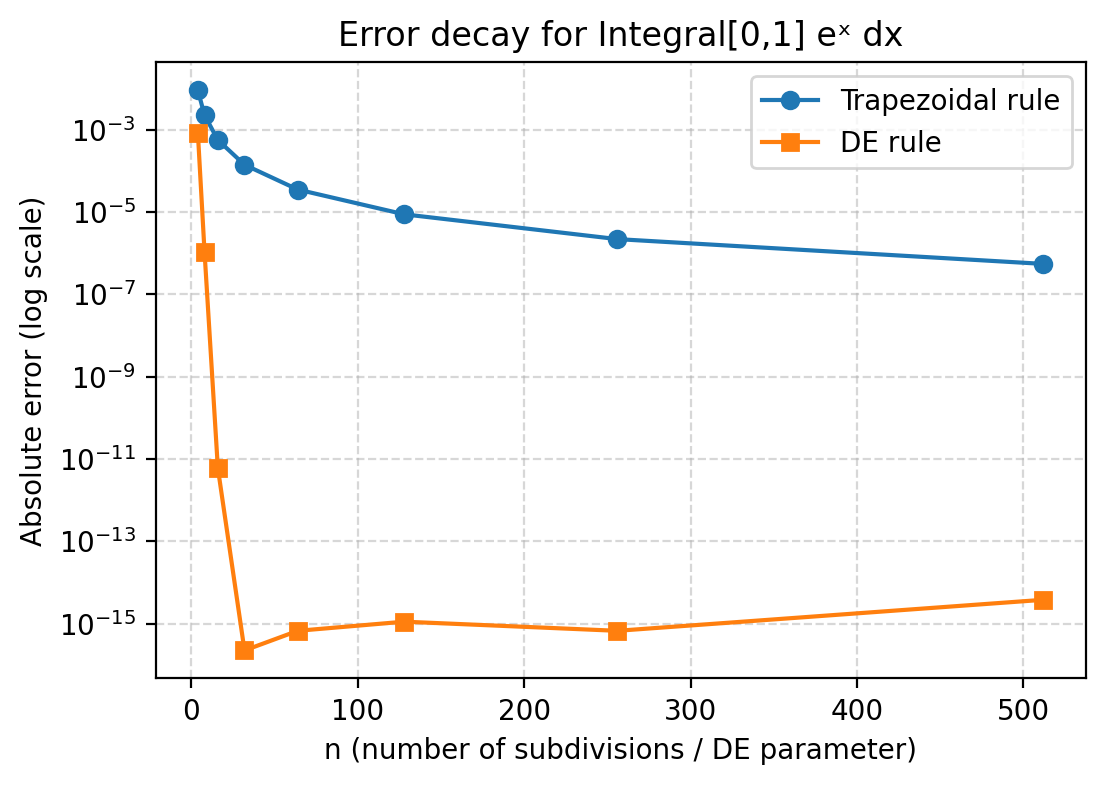
• 台形公式(青)
  分点数$n$を増やすと徐々に誤差が減衰していきますが、その減衰速度は速くありません。
  理論的には台形公式の誤差は $$\begin{aligned} O\left(\frac{1}{n^{2}}\right) \end{aligned}$$ の多項式的な収束を示し、実際グラフでもほぼ直線的に下がる緩やかな減衰 になっています。
• DE公式(橙)
  小さな$n$でも誤差が急激に減衰し、$n=16$を超えたあたりで早くも$10^{-15}$(倍精度浮動小数点数が保持できる桁の限界付近) に達しています。
  これはDE公式の誤差が $$\begin{aligned} O(\exp(-cn)) \end{aligned}$$ のような指数的収束 を示すためで、台形公式と比べて圧倒的に早く収束することがわかります。
• 全体の比較
  台形公式は分点数$n$を増やすほど少しずつ精度が上がるのに対し、DE公式は極めて少ない分点数で機械精度に達するほど高効率です。
  滑らかな関数$e^{x}$に対しても、DE公式が非常に高い性能を発揮することを示しています。

区間演算による精度保証について

台形公式やDE公式はいずれも数値的な近似手法であり積分値を厳密に求める際には、何らかの誤差が含まれます。

• 台形公式では主に離散化誤差(刻み幅による誤差)
• DE公式では離散化誤差に加えて変数変換後の全無限の積分区間を有限区間で「打ち切る」ことによる打ち切り誤差

これらの誤差が理論的に存在します。

精度保証付き数値計算(Verified Numerics) を実現するためには、これらすべての誤差要因を厳密に評価し、最終結果を区間として包含する必要があります。

しかし、誤差項の理論的扱いは非常に高度であり、特にDE公式のように変数変換を伴う手法では、誤差の評価式そのものが複雑になります。

そのため、ここでは詳細な理論展開には踏み込みません。
精度保証付き数値計算を本格的に学びたい方のために、参考となる書籍のみ紹介することにします。

📘精度保証付き数値計算の基礎

まとめ

この記事では、数値積分の基本である台形公式と積分区間の端点の特異点や無限区間の積分にも対応できる高精度な手法であるDE(Double Exponential)公式を紹介しました。

• 台形公式はシンプルで実装しやすい反面、収束は多項式的で、特異点には弱い
• DE公式は変数変換によって積分区間の端点の特異点を無限遠点へ押し出し、指数的な収束を実現する非常に強力な手法
• DE公式を実装する際には桁落ちやオーバーフローを避けるために式変形が必要なことがある
• 精度保証を行うには、離散化誤差・打切り誤差などの理論的な誤差を数学的に評価し、区間演算で包含する必要がある

現代の数値計算では「解析的に積分できない関数」のほうが一般的です。
そのため、数値積分の基礎を理解し、適切な方法を選択できることは非常に重要です。

台形公式のような基本的な手法だけでなく、DE公式のような高精度手法まで理解しておくと、実際の科学技術計算・統計計算・シミュレーションなどで大きな力になります。